Das Mierscheid-Walla-Gesetz
Der dienstälteste Bundestagsabgeordnete, Katholik, Witwer und Flugtaubenexperte Jakob Maria Mierscheid (73) veröffentlichte bereits im Jahr 1983 seine richtungweisende Erkenntnis, dass die Bundestagswahlergebnisse für die SPD stark mit der Produktionsmenge für Rohstahl korrelieren. Den passionierten Taubenzüchter und statistischen Autodidakten zeichnete ein enormes statistisch-stochastisches Gespür aus. Bemerkenswert ist, dass sich die amtliche und wissenschaftliche Statistik seiner fundamentalen Entdeckung nur zaghaft nähern. In diesem Beitrag soll daher – auch zum Dank – belegt werden, dass sich das Mierscheid-Gesetz verallgemeinern lässt.
Wie leicht einzusehen, lassen sich die Wahlergebnisse zusammenfassend wie folgt darstellen:
| W(k,p,t) | = | ∑(k=1,2,…,k)>, ∑(p=1,2,…,p), ∑(t=1,2,…,t) (Gk,p,t + Uk,t + Nk,t + Ek,p,t) |
Wobei:
| W | := | Wahlberechtigte (sofern als solche bekannt) > 0 |
| G | := | gültig Wählende (absichtlich oder unabsichtlich) = 0 |
| U | := | ungültig Wählende (absichtlich oder unabsichtlich) = 0 |
| N | := | nicht Wählende (aber als wahlberechtigt bekannt) = 0 |
| E | := | Fehler des Wahlvorstandes eines Stimmbezirks (in der Regel unbekannt) = 0 oder < 0 |
| k | := | Stimmbezirk 1,2,…,k, oder Bundesland 01,02,…,11. Da Mierscheid sich nur auf die Ergebnisse der alten BRD insgesamt bezieht, wird im Weiteren auf die Variable k verzichtet, was methodisch nicht von Nachteil ist. |
| p | := | Partei 1,2,…,p, wegen der novaistischen Effekte mancher Parteien sind die Werte nicht > 0 sondern = 0 |
| t | := | Bundestagswahl (BTW) 1,2,…,t, T ≥ 1949 |
Für die bis 2005 durchgeführten Bundestagswahlen ergibt sich ein zusammenfassendes W von 379 754 291.
Ein eher pragmatischer Ansatz für die Partei p bei der Wahl t, der zudem den amtlichen Wahlergebnissen entspricht, ist:
| y(p,t) | = | g(p,t) * (∑(p=1,2,…,P,t) gp,t)−1 * 100 |
Mierscheid ahnte, dass für die SPD speziell gilt:
| y(p= SPD) | = | f(t) und |
| x(Stahl) | = | f(t) |
wobei:
| x | := | Stahlproduktion in Tonnen1, erste dependente Variable, |
| y | := | gültige Stimmen einer Partei p, zweite dependente Variable, |
| t | := | Zeitpunkt t (BTW), independente Variable. |
Mierscheid erkannte die Parallelität zweier Zeitvariablen und deutete die korrelative Interdependenz an, wie seine berühmte Grafik2 verdeutlicht (Schaubild 1).
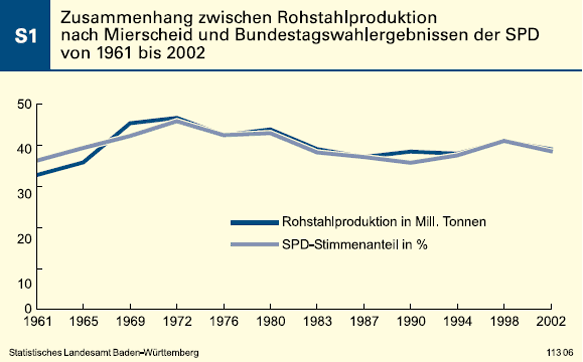
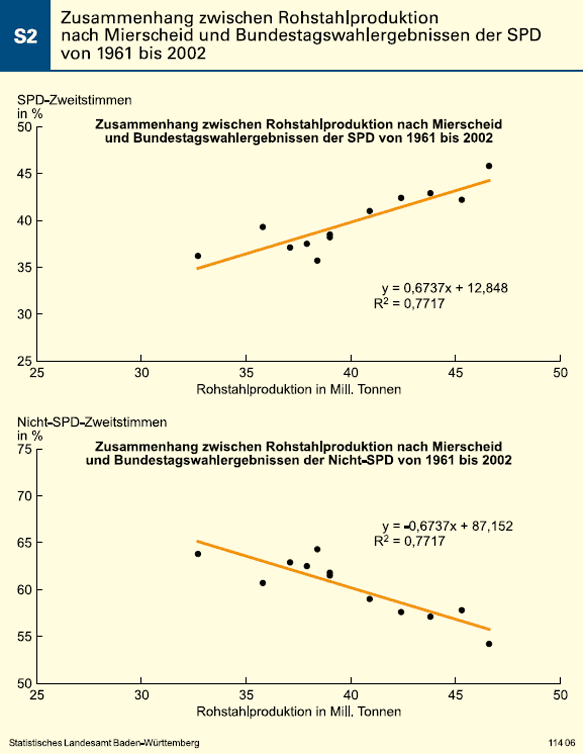
Die von Mierscheid entdeckten Abhängigkeiten lassen sich adäquater wie folgt darstellen (Schaubild 2):
| y(SPD) | = | f(x(Stahl)) |
Dabei ergibt sich ein Regressionskoeffizient von r = 0,6737 und ein Korrelationskoeffizient von 0,5956. Das heißt, eine zusätzliche Mill. Tonnen Stahl entspricht mit einer Bestimmtheit von 77 % einem zusätzlichen SPD-Stimmenanteil von 0,7 %. Weiter bedeutet das Ergebnis, dass die SPD auch ohne jede Stahlproduktion in Deutschland 13 % der Zweitstimmen erhält. Eine Schwäche des originären Mierscheid-Gesetzes liegt in der mangelnden zeitlichen Äquidistanz der Bundestagswahlen3 und in den divergierenden Zahlen der Wahlberechtigten4.
Nicht nur wahlanalytisch muss gefragt werden, ob der Niedergang der Stahl- und Hüttenindustrie an Saar oder Ruhr letztlich für die SPD zum Verlust der Regierungsmacht an Saar und Ruhr führten. Das wiederum lässt für Methodiker die Frage aufkommen, durch welches Item die Stahlproduktion substituiert werden kann, wenn in Deutschland eines Tages nur noch in Kehl (Baden-Württemberg) Stahl produziert werden sollte. Das Statistische Landesamt Baden-Württemberg hat daher umfangreiche Faktorenanalysen durchgeführt, um informational relevante Substitute für die independente Variable x zu finden. Die Ergebnisse sind vielversprechend: Hohe – allerdings negative – Abhängigkeiten ließen sich mit den Faktoren Exportwert von Automobilen sowie vom Beschäftigungsniveau des humaninfrastrukturellen Bereichs der Rechtsberatung feststellen. Deutliche und ebenfalls negative Abhängigkeiten ergaben sich für die bürgerlichen Parteien vom Kaffeepreis und der Anzahl der Autounfälle auf Innerortsstraßen; dabei dürfte es sich eher um Scheinkorrelationen handeln. Die Forschungsarbeiten sind hier allerdings noch nicht abgeschlossen.
Aufgrund dieser ersten Erkenntnisse konnten zwei allgemeine Forderungen an ein modifiziertes und allgemein gültiges Mierscheid-Modell gestellt werden:
- Die abgegebenen gültigen Stimmen müssen parteiunabhängig im Modell ihren Niederschlag finden.
- Die Produktion ist nicht im metrischen KMS-System, sondern mit dem Geldwert der Bruttowertschöpfung eines Wirtschaftszweiges5 zu messen.
Daraus ergibt sich, wie sofort einzusehen, das Allgemeine Mierscheid-Walla-Gesetz:
| y | = | f(x) |
Der ersten der obigen Forderungen ist relativ simpel mit den Rechentechniken von Georg Ferdinand Ludwig Philipp Cantor beizukommen, denn es gilt:
| W | = | U {G,U,N,E} |
Da U, N und E in Deutschland6 und diesem Zusammenhang nicht relevant und die Teilmengen Gp disjunkt sind, lässt sich vereinfachen:
| G | = | U {G1,G2, … Gn} |
Dann gilt:
| {Gp} | = | G − U {G1,G2, … Gn ∕ Gp} |
Im mathematisch idealtypischen Falle einer Zweiparteienlandschaft würde für die Summe der gültigen Stimmen gelten:
| {Gp} | = | {G1, G1‾} oder |
| {Gp} | = | {G1, G2} |
Das heißt Gp sind alle jene, die die Partei G1 gewählt haben plus dem Komplement derer; das sind alle jene, die die Partei G1 nicht, sondern G2 gewählt haben. Mierscheids Erkenntnis ließe sich bezüglich der SPD und CDU dann wie folgt darstellen:
| {Gp} | = | {GSPD, GSPD‾} oder |
| {Gp} | = | {GSPD, GCDU} |
Daraus lässt sich über das Allgemeine Mierscheid-Walla-Gesetz leicht und unmittelbar ableiten:
| y(SPD) | = | f(x) | = | + mx + a und |
| y(CDU) | = | g(x) | = | − mx + b |
Um auf Mierscheids bewundernswerte Sprachebene zurückzukommen: »Der Erfolg der SPD ist von der Stahlproduktion abhängig und der Erfolg der CDU von der Nichtstahlproduktion«7.
Die zweite Forderung nach der in Geldeinheiten bewerteten Bruttowertschöpfung (BWS) scheint einfach zu sein, ist es aber nicht. Leider lässt sich der Beitrag zum Beispiel von Innerortsunfällen zur BWS nicht ohne Weiteres in Geldeinheiten darstellen. Hier ist die CB-Analysis8 gefordert. Ausgewählte Analytiker versuchen derzeit den volkswirtschaftlichen Nutzen von Autounfällen zu berechnen. Darüber hinaus wird versucht, renommierte Lehrstühle zu gewinnen, die diesen Problemkreis im Rahmen von Diplomarbeiten oder Dissertationen zu erforschen bereit sind.
Der Versuch die Oszillationen mit Hilfe von Kondratieff-Zyklen zu beschreiben, ist bislang misslungen. Die Spannweite der Zeitreihen im Sinne von tmax – tmin sind zu kurz. Frühestens nach der Wahl zum 63. Bundestags lassen sich derartige Forschungen fortsetzen. Wegen der mangelnden temporären Äquidistanzen zwischen den BTW kann der Beginn diesbezüglicher Arbeit nicht exakt bestimmt werden.